Graph Traversal with Clojure

I’m going through the Coursera Algorithms I class in my spare time. Like most of my experiences with Coursera I signed up for the course with little expectation of doing the course but wanting to unlock all of the videos and other material for perusal later. So I suck at MOOCs.

I’m on the course section covering graphs. Graphs are awesome and its a nice step up from sorting. I want to take a shot at implementing some graph algorithms using Clojure and figure a good starting point would be graph traversal using breadth first search and depth first search.

WARNING: I am no Clojure expert!

My starting point was creating a function which would traverse a graph and print out each node as it went. I had no idea what I wanted to do so debug print statements seemed as good as any. Then I thought it would be much cooler to have a function passed in which would get called on each node as it traversed the graph. Then I realized I’m implementing my own map function and that I’m probably wrong.

In order to get Clojure’s built in map function to work with the graph I would need to turn it into a sequence. Ah, now that seems like a reasonable idea.

Here is how I’m representing a graph.

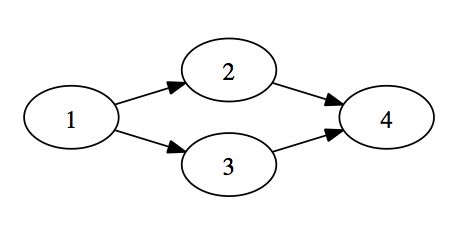
(def G {
        :1 [:2 :3],
        :2 [:4],
        :3 [:4],
        :4 [] })

The graph structure is a map of nodes to a list of neighbors. So { :1 [:2 :3] } means :1 has two edges – one to :2 and one to :3. Here is my very first ever graphviz!

graphviz

And here is my go at doing a depth first search on a graph returning a sequence (vector in this case).

(defn traverse-graph-dfs [g s]
  (loop [vertices [] explored #{s} frontier [s]]
    (if (empty? frontier)
      vertices
      (let [v (peek frontier)
            neighbors (g v)]
        (recur
          (conj vertices v)
          (into explored neighbors)
          (into (pop frontier) (remove explored neighbors)))))))

(traverse-graph-dfs G :1) ; => [:1 :3 :4 :2]

The course describes the algorithm recursively so I’m using Clojure’s loop and recur syntax. In the loop we want to keep track of three things:

a built up vector of traversed vertices
a set of explored vertices (explored means we have seen it)
a stack of frontier vertices (frontier means we have explored it but haven’t explored its neighbors)

In the initial case we have an empty vector of traversed vertices, an explored set including our starting vertex and a frontier stack including our starting vertex.

On each iteration we check if the frontier stack is empty. If it is we are done and return the traversed vertices. If not we pop the stack for a vertex and get the vertex’s neighbors. We then recurse adding the vertex to the traversed vertices, adding the neighbors to the explored set, and adding the unexplored neighbors to the frontier.

This works but its eager – the graph is fully traversed when you call the function. I wanted to try and make a lazy sequence version. In order to do this I use the magic of lazy-seq.

(defn seq-graph-dfs [g s]
  ((fn rec-dfs [explored frontier]
     (lazy-seq
       (if (empty? frontier)
         nil
         (let [v (peek frontier)
               neighbors (g v)]
           (cons v (rec-dfs
                     (into explored neighbors)
                     (into (pop frontier) (remove explored neighbors))))))))
   #{s} [s]))

(seq-graph-dfs G :1) ; => (:1 :3 :4 :2)

Instead of loop and recur we define a recursive function, rec-dfs, and use lazy-seq to build up the sequence with recursive calls. Each call cons the current vertex to the result of a new recursive call finally ending with a nil (end of sequence). Through the magic of lazy-seq we don’t have to worry about blowing the stack and get the benefits of the sequence being lazy. This means if I take 2 from the sequence we only traverse 2 nodes, not the entire graph as we would have done in traverse-graph-dfs.

(take 2 (seq-graph-dfs G :1)) ; => (:1 :3)

Here is a wiki page describing an implementation of Fibonacci using lazy-seq which might be easier to follow as the algorithm is more instantly recognizable.

With DFS working I wanted to try BFS. Luckily the change is simple – just change the stack to a queue.

(defn seq-graph-bfs [g s]
  ((fn rec-bfs [explored frontier]
     (lazy-seq
       (if (empty? frontier)
         nil
         (let [v (peek frontier)
               neighbors (g v)]
           (cons v (rec-bfs
                     (into explored neighbors)
                     (into (pop frontier) (remove explored neighbors))))))))
   #{s} (conj (clojure.lang.PersistentQueue/EMPTY) s)))

(seq-graph-bfs G :1) ; => (:1 :2 :3 :4)

This works because all the primitives (peek, pop, conj) do the right things depending on the data structure (stack or queue). It was nice to see this actually work.

Finally, since the only difference is the initial data structure we can make it an argument to a generic function.

(defn seq-graph [d g s]
  ((fn rec-seq [explored frontier]
     (lazy-seq
       (if (empty? frontier)
         nil
         (let [v (peek frontier)
               neighbors (g v)]
           (cons v (rec-seq
                     (into explored neighbors)
                     (into (pop frontier) (remove explored neighbors))))))))
   #{s} (conj d s)))

(def seq-graph-dfs (partial seq-graph []))
(def seq-graph-bfs (partial seq-graph (clojure.lang.PersistentQueue/EMPTY)))

(seq-graph-dfs G :1) ; => (:1 :3 :4 :2)
(seq-graph-bfs G :1) ; => (:1 :2 :3 :4)

Neato.

Again, I’m no Clojure expert so welcome feedback on anything that can do better.